| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- C++
- nestjs typeorm
- Spring
- nestjs auth
- 해시
- C언어
- 스프링
- AWS
- spring boot
- 카카오 코테
- git
- @Autowired
- Nodejs
- TypeORM
- 카카오 알고리즘
- 코테
- python
- 프로그래머스
- 알고리즘
- nestJS
- 시스템호출
- @Component
- 카카오
- 파이썬
- 가상면접사례로배우는대규모시스템설계기초
- OpenCV
- 구조체배열
- 컴포넌트스캔
- thymeleaf
- 코딩테스트
- Today
- Total
공부 기록장 💻
[자료구조] 다항식 배열의 연산 (구조체 배열, 포인터, 다항식의 표현) 본문
(C언어로 쉽게 풀어쓴 자료구조 ch 3.3)
다항식의 표현
p(x) = a(x)^n
a : 계수
x : 변수
n : 차수
구조체와 배열을 이용하여
다항식을 표현하는 두 가지 자료 구조를 알아보고,
덧셈 연산을 이용해 두 다항식에 대한 결과 값을 저장하는 방법을 살펴보자
< 첫번째 자료 구조 >
최고 차항의 차수와 배열을 멤버로 갖는 구조체로 표현하여
하나의 다항식의 모든 항을 저장하는 구조체 변수로 선언하는 방법
계수가 0인 차항을 포함하여, 모든 차항의 계수값들을 배열 coef에 저장한다.
- 단점: 계수가 0인 희소 다항식의 경우엔 공간의 낭비가 심하다.
- 장점: 덧셈이나 뺄셈 연산 시, 같은 차수의 계수를 쉽게 찾을 수 있으므로 알고리즘은 간단하다.
#include <stdio.h>
#define _CRT_SECURE_NO_WARNINGS
#define MAX(a,b) (((a)>(b))?(a):(b))
#define MAX_DEGREE 101
typedef struct {
int degree;
float coef[MAX_DEGREE];
}polynomial;
polynomial poly_add1(polynomial A, polynomial B) {
polynomial C;
int Apos = 0, Bpos = 0, Cpos = 0;
int degree_a = A.degree;
int degree_b = B.degree;
C.degree = MAX(A.degree, B.degree);
while (Apos <= A.degree && Bpos <= B.degree) {
if (degree_a > degree_b) {
C.coef[Cpos++] = A.coef[Apos++];
degree_a--;
}
else if (degree_a == degree_b) {
C.coef[Cpos++] = A.coef[Apos++] + B.coef[Bpos++];
degree_a--;degree_b--;
}
else {
C.coef[Cpos++] = B.coef[Bpos++];
degree_b--;
}
}
return C;
}
void print_poly(polynomial p) {
for (int i = p.degree;i > 0;i--)
printf("%3.1f x^%d + ", p.coef[p.degree - i], i);
printf("%3.1f \n", p.coef[p.degree]);
}
int main(void) {
// 구조체 배열을 미리 선언
polynomial a = { 5,{3,6,0,0,0,10} };
polynomial b = { 4,{7,0,5,0,1} };
polynomial c;
print_poly(a);
print_poly(b);
c = poly_add1(a, b);
printf("-----------------------------------------------------\n");
print_poly(c);
return 0;
}
구조체 배열은 정수(최고 차항의 차수)와 실수형 배열의 멤버들로 이루어져 있다.
두 다항식을 더할 때, 최고 차항의 차수부터 시작하여 각 항의 차수를 비교하여
새로운 구조체 배열에 어떠한 값을 대입할지 결정할 수 있다. (while반복문 내의 조건문 활용)
poly_add1 함수에서 최고 차항의 계수부터 배열에 저장됨을 확인할 수 있다.
Apos와 Bpos의 값이 바뀌며 해당 인덱스에 저장된 값이
C 구조체 배열에 차곡차곡 차례대로 저장되는 것을 볼 수 있다.
** 구조체 배열의 멤버(정수, 배열) 사용자로부터 입력 받기
** 각 차항의 계수가 배열에 저장될 때 마다 출력하여 값 확인하기
#include <stdio.h>
#define _CRT_SECURE_NO_WARNINGS
#define MAX(a,b) (((a)>(b))?(a):(b))
#define MAX_DEGREE 101
typedef struct {
int degree;
float coef[MAX_DEGREE];
}polynomial;
polynomial poly_add1(polynomial A, polynomial B) {
polynomial C;
int Apos = 0, Bpos = 0, Cpos = 0;
int degree_a = A.degree;
int degree_b = B.degree;
C.degree = MAX(A.degree, B.degree);
while (Apos <= A.degree && Bpos <= B.degree) {
if (degree_a > degree_b) {
printf("%d차항 : C.coef[%d] = A.coef[%d] = %d \n", degree_a, Cpos, Apos, (int)A.coef[Apos]);
C.coef[Cpos++] = A.coef[Apos++];
degree_a--;
}
else if (degree_a == degree_b) {
printf("%d차항 : C.coef[%d] = A.coef[%d] + B.coef[%d] = %d \n", degree_a, Cpos, Apos, Bpos, (int)(A.coef[Apos] + B.coef[Bpos]));
C.coef[Cpos++] = A.coef[Apos++] + B.coef[Bpos++];
degree_a--;degree_b--;
}
else {
printf("%d차항 : C.coef[%d] = B.coef[%d] = %d \n", degree_b, Cpos, Bpos, (int)B.coef[Bpos]);
C.coef[Cpos++] = B.coef[Bpos++];
degree_b--;
}
}
return C;
}
void print_poly(polynomial p) {
for (int i = p.degree;i > 0;i--)
printf("%3.1f x^%d + ", p.coef[p.degree - i], i);
printf("%3.1f \n", p.coef[p.degree]);
}
int main(void) {
/*
polynomial a = { 5,{3,6,0,0,0,10} };
polynomial b = { 4,{7,0,5,0,1} };
polynomial c;
*/
// 직접 다항식 정보 입력 받기
polynomial a, b, c;
printf("[첫번째 다항식 정보 입력]\n\n");
printf("최고차항의 차수 : ");
scanf("%d", &a.degree);
printf("순서대로 차항의 계수 입력 : ");
for (int i = 0;i <= a.degree;i++)
scanf("%f", &a.coef[i]);
printf("\n첫번째 다항식 : ");
print_poly(a);
printf("\n\n[두번째 다항식 정보 입력]\n\n");
printf("최고차항의 차수 : ");
scanf("%d", &b.degree);
printf("순서대로 차항의 계수 입력 : ");
for (int i = 0; i<=b.degree;i++)
scanf("%f", &b.coef[i]);
printf("\n두번째 다항식 : ");
print_poly(b);
printf("\n");
print_poly(a);
print_poly(b);
printf("\n");
c = poly_add1(a, b);
printf("----------------------------------------------------------\n");
print_poly(c);
return 0;
}
결과:
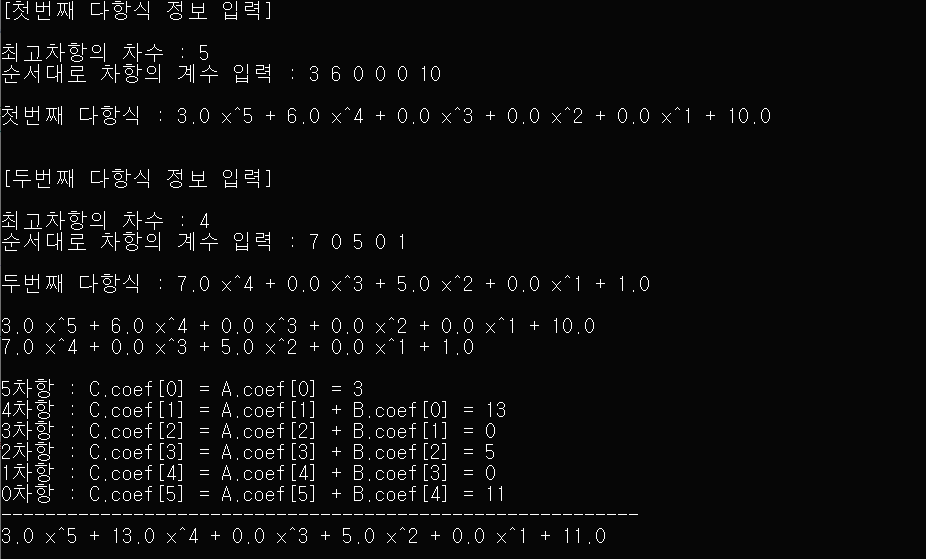
** 두 다항식에 대한 연산 후, 최고 차항의 계수의 합이 0인 경우
아래 예시와 같이 최고 차항의 차수를 5로 갖는 두 다항식의 최고 차항의 계수는 각각 -3과 3이므로
연산의 합은 0이 되어 최고 차항의 결과 값이 0.0 x^5 으로 출력된다.
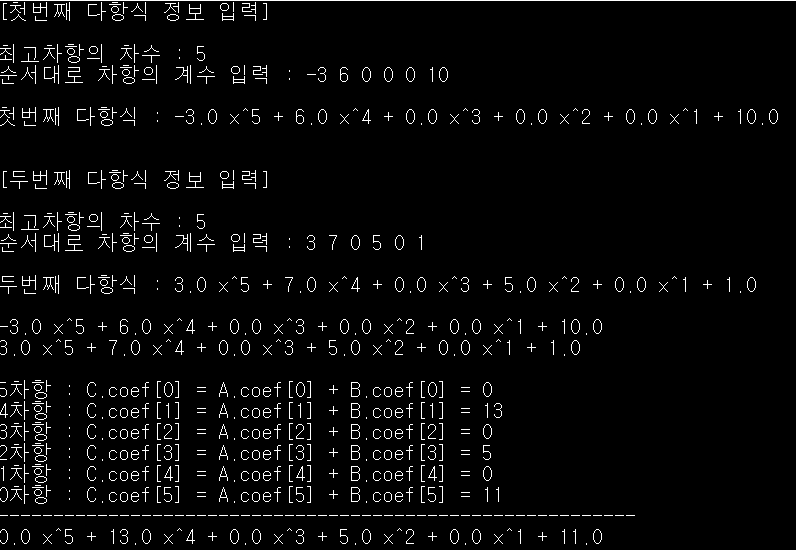
최고 차항의 계수가 0으로 결과 값이 나오는 경우를 처리하기 위해
다음과 같이 print_poly 함수에 간단한 코드 세 줄을 추가했다. (이 방법 말고는 생각이 안 났다.)
void print_poly(polynomial p) {
if(p.coef[0])
printf("%3.1f x^%d + ", p.coef[0], p.degree);
for (int i=1;i <p.degree;i++)
printf("%3.1f x^%d + ", p.coef[i], p.degree-i);
printf("%3.1f \n", p.coef[i]);
}
함수의 배열 멤버의 첫번째 요소(최고 차항의 계수)가 0이 아닌 경우에만 해당 항을 출력하도록 만들었다.
그리고 다음 반복문의 제어 변수 i를 1부터 증가하도록 만들었고,
항을 표현하는 식을 조금 변형하였다.
다음과 같이 최고 차항이 차수 4부터 시작됨을 확인할 수 있다.

** 파일에 저장된 다항식을 읽는 함수 poly_read 추가 구현
이번에는 구조체를 직접 초기화 하거나, 사용자로부터 입력 받는 방법이 아닌
파일에 다항식에 대한 정보가 저장되어 있을 때 이를 읽어 다항식의 연산을 하는 방법이다.
data.txt 파일을 생성하여 다음과 같이 두 구조체 배열의 데이터를 저장해 놓았다.

main함수에서는 다음과 같이 세 개의 구조체를 선언하고,
a와 b의 주소를 인수로 전달하며 poly_read 함수를 호출한다.
// 파일에 저장된 다항식 읽기
polynomial a, b, c;
poly_read(&a, &b);
다항식에 대한 두 구조체의 주소를 매개 변수로 받아 오는 poly_read 함수를 다음과 같이 구현하였다.
파일 포인터는 해당 함수 내에서 선언하여 열고 닫을 수 있도록 하였다.
가장 먼저 최고 차항의 계수를 멤버 변수 degree에 저장하게 되고,
이 값에 해당하는 크기만큼 파일로부터 다음 정수들을 읽어 배열에 저장하는 방식이다.
void poly_read(polynomial *a, polynomial *b) {
FILE* fp;
fp = fopen("data.txt", "rt");
if (fp == NULL) {
printf("File not found\n");
return 0;
}
// 파일로부터 각 다항식의 최고 차항 차수를 읽어 그 값의 크기만큼 정수들을 coef배열에 저장
fscanf(fp, "%d", &a->degree);
printf("%d \n", a->degree);
for (int i = 0; i <= a->degree; i++) {
fscanf(fp, "%f", &a->coef[i]);
printf("a->coef[%d] = %3.1f\n", i, a->coef[i]);
}
fscanf(fp, "%d", &b->degree);
printf("\n%d\n", b->degree);
for (int i = 0; i <= b->degree; i++) {
fscanf(fp, "%f", &b->coef[i]);
printf("b->coef[%d] = %3.1f\n", i, b->coef[i]);
}
fclose(fp);
}
구조체 포인터를 사용하였으므로, -> 멤버 연산자를 이용하고
데이터를 입력 받는 경우에는 꼭 & 주소 연산자를 붙여 주는 것을 까먹지 말자!!
결과는 다음과 같다.
배열에 정수들이 올바르게 저장되는지 확인하기 위해 각 값을 출력하여 확인해보았다.

< 두번째 자료 구조 >
차수와 계수를 멤버 변수로 갖는 구조체에 대한 배열을 선언하여
모든 다항식의 0이 아닌 항을 한 배열에 저장하는 방법
두 다항식을 더하는 두번째 방법은
0이 아닌 항만을 하나의 전역 배열에 저장하는 방법이다.
해당 항을 (계수, 차수) 쌍으로 이루어진 구조체를 선언하여 이 구초제에 대한 1차원 배열에
첫번째 다항식, 두번째 다항식, 그리고 연산된 세번째 다항식의 데이터값을 차곡차곡 저장하는 방법이다.
- 장점: 세 다항식에 대한 모든 항의 개수가 일정 개수를 넘지만 않으면 많은 다항식을 공간을 낭비하지 않고 저장 가능
- 단점
- 하나의 다항식이 시작되고 끝나는 위치를 가리키는 인덱스 변수들을 관리해야 한다는 점
- 차수도 구조체의 한 멤버로서 저장해야 한다는 점에서 0이 아닌 항이 많은 다항식인 경우 공간을 많이 차지할 수도 있다는 점
- 그리고 연산 구현이 복잡하다는 점
#include <stdio.h>
#include <stdlib.h>
#define MAX_TERMS 101
typedef struct polynomial {
float coef; // 계수
int expon; // 차수
}Poly;
// 구조체 배열 선언
Poly terms[MAX_TERMS] = { {8,3}, {7,2}, {1,1}, {10,3}, {3,2}, {1,0} };
int avail=6;
// 두 정수 비교
char compare(int a, int b) {
if (a > b)return '>';
else if (a == b) return '=';
else return '<';
}
// 새로운 항을 다항식에 추가
void attach(float coef, int expon) {
if (avail > MAX_TERMS) {
fprintf(stderr, "항의 개수가 너무 많음 \n");
exit(1);
}
terms[avail].coef = coef;
terms[avail].expon = expon;
avail++;
}
// C = A + B
void poly_add2(int As, int Ae, int Bs, int Be, int* Cs, int* Ce) {
float temcoef;
*Cs = avail; // 항목이 추가될 배열의 인덱스 번호
while (As <= Ae && Bs <= Be)
switch (compare(terms[As].expon, terms[Bs].expon)) {
case '>':
attach(terms[As].coef, terms[As].expon);
As++;
break;
case '=':
temcoef = terms[As].coef + terms[Bs].coef;
if (temcoef)
attach(temcoef, terms[As].expon);
As++;Bs++;
break;
case '<':
attach(terms[Bs].coef, terms[Bs].expon);
Bs++;
default:break;
}
for (;As < Ae;As++)
attach(terms[As].coef, terms[As].expon);
for (;Bs <= Be;Bs++)
attach(terms[Bs].coef, terms[Bs].expon);
*Ce = avail - 1;
}
void print_poly(int s, int e) {
for (int i = s;i < e;i++)
printf("%3.1f x^%d + ", terms[i].coef, terms[i].expon);
printf("%3.1f x^%d \n", terms[e].coef, terms[e].expon);
}
int main(void) {
int As = 0, Ae = 2, Bs = 3, Be = 5, Cs, Ce; // 인덱스 번호
poly_add2(As, Ae, Bs, Be, &Cs, &Ce);
printf("\n");
print_poly(As, Ae);
print_poly(Bs, Be);
printf("---------------------------------------------------------\n");
print_poly(Cs, Ce);
return 0;
}
poly_add2 함수에서 인덱스 번호 As-Ae 사이의 값들에 해당하는 다항식과
Bs-Be 사이의 값들에 해당하는 다항식의 각 차수를 비교하여 compare 함수를 이용해 얻은 비교 결과의 문자형에 따라
조건에 맞게 attach함수에 전달하는 계수, 차수의 매개변수 값을 다항식 A 또는 B의 것으로 결정하게 된다.
0이 아닌 항이 적을 경우, 메모리 공간을 적게 차지 한다는 점에서 매우 효율적이지만
연산이 정말 복잡하고 추가적으로 필요한 변수들도 많다.
구조체 배열과 새로 추가되는 항에 대한 구조체 배열의 인덱스 번호를 전역으로 설정하여 값을 관리해야 한다는 점에서, 변수에 대한 관리가 쉽지 않다.
** 각 연산이 이루어질 때, 구조체 배열의 인덱스 번호 값을 출력하여 확인
#include <stdio.h>
#include <stdlib.h>
#define MAX_TERMS 101
typedef struct polynomial {
float coef; // 계수
int expon; // 차수
}Poly;
// 구조체 배열 선언
Poly terms[MAX_TERMS] = { {8,3}, {7,2}, {1,1}, {10,3}, {3,2}, {1,0} };
int avail=6;
// 두 정수 비교
char compare(int a, int b) {
if (a > b)return '>';
else if (a == b) return '=';
else return '<';
}
// 새로운 항을 다항식에 추가
void attach(float coef, int expon) {
if (avail > MAX_TERMS) {
fprintf(stderr, "항의 개수가 너무 많음 \n");
exit(1);
}
terms[avail].coef = coef;
terms[avail].expon = expon;
printf("C[%d](%3.1f x^%d)\n", avail, terms[avail].coef, terms[avail].expon);
avail++;
}
// C = A + B
void poly_add2(int As, int Ae, int Bs, int Be, int* Cs, int* Ce) {
float temcoef;
*Cs = avail; // 항목이 추가될 배열의 인덱스 번호
while (As <= Ae && Bs <= Be)
switch (compare(terms[As].expon, terms[Bs].expon)) {
case '>':
printf("A[%d](%3.1f x^%d) => ",As,terms[As].coef, terms[As].expon );
attach(terms[As].coef, terms[As].expon);
As++;
break;
case '=':
printf("A[%d](%3.1f x^%d) + B[%d](%3.1f x^%d) => ", As, terms[As].coef, terms[As].expon,Bs, terms[Bs].coef, terms[Bs].expon);
temcoef = terms[As].coef + terms[Bs].coef;
if (temcoef)
attach(temcoef, terms[As].expon);
As++;Bs++;
break;
case '<':
printf("B[%d](%3.1f x^%d) => ", Bs, terms[Bs].coef, terms[Bs].expon);
attach(terms[Bs].coef, terms[Bs].expon);
Bs++;
default:break;
}
for (;As < Ae;As++) {
printf("A remained[%d](%3.1f x^%d) => ", As, terms[As].coef, terms[As].expon);
attach(terms[As].coef, terms[As].expon);
}
for (;Bs <= Be;Bs++) {
printf("B remained[%d](%3.1f x^%d) => ", Bs, terms[Bs].coef, terms[Bs].expon);
attach(terms[Bs].coef, terms[Bs].expon);
}
*Ce = avail - 1;
}
void print_poly(int s, int e) {
for (int i = s;i < e;i++)
printf("%3.1f x^%d + ", terms[i].coef, terms[i].expon);
printf("%3.1f x^%d \n", terms[e].coef, terms[e].expon);
}
int main(void) {
int As = 0, Ae = 2, Bs = 3, Be = 5, Cs, Ce; // 인덱스 번호
poly_add2(As, Ae, Bs, Be, &Cs, &Ce);
printf("\n");
print_poly(As, Ae);
print_poly(Bs, Be);
printf("---------------------------------------------------------\n");
print_poly(Cs, Ce);
return 0;
}
결과 :
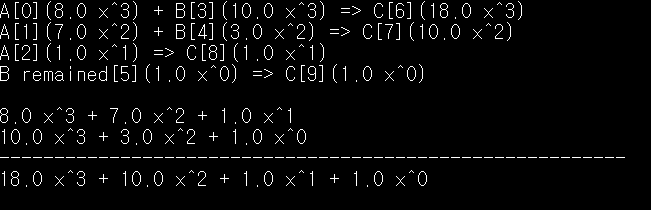
'# CS Study > DS Algorithm' 카테고리의 다른 글
| [자료구조] 단순 연결 리스트(Linked List) ADT + 예제들 (1) | 2021.04.14 |
|---|---|
| [자료구조] 단순 연결 리스트 Singly Linked List 실습 문제 - 동적 메모리 할당, 노드 생성(create), 삽입(insert), 역순 연산(reverse), 버블 정렬(bubble sort), 출력, 메모리 해제 (0) | 2021.04.13 |
| [자료구조] 배열 실습 문제들 (0) | 2021.04.04 |
| [자료구조] 연도별 통계 프로그램 (2차원 배열, 반복문) (0) | 2021.03.15 |
| [자료구조] 성적 관리 프로그램 (2차원 배열, 파일 입출력, 반복문 활용) (0) | 2021.03.14 |

