| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- OpenCV
- 시스템호출
- thymeleaf
- nestJS
- 카카오 코테
- 파이썬
- 가상면접사례로배우는대규모시스템설계기초
- @Autowired
- 코테
- Spring
- 프로그래머스
- 해시
- TypeORM
- Nodejs
- @Component
- AWS
- spring boot
- 구조체배열
- nestjs typeorm
- 알고리즘
- 카카오 알고리즘
- git
- 카카오
- 스프링
- C언어
- python
- 컴포넌트스캔
- C++
- 코딩테스트
- nestjs auth
- Today
- Total
공부 기록장 💻
[OpenCV/C++] 에지 검출 4 응용 - 허프 변환 직선, 원 검출 (Line and Circle Detection Using Hough Transform) 본문
[OpenCV/C++] 에지 검출 4 응용 - 허프 변환 직선, 원 검출 (Line and Circle Detection Using Hough Transform)
dream_for 2022. 12. 3. 22:14OpenCV 4로 배우는 영상 처리와 컴퓨터 비전 CH9. 에지 검출과 응용 정리
이번엔 영상에서 추출한 에지 정보를 이용해 영상에서 직선 또는 원을 검출해보자.
컴퓨터 비전에서 직선 검출은 주로 허프변환 기법을 사용한다. 기본적인 허프 변환 이론과 직선 검출에 적용되는 방법, 그리고 원을 검출하기 위해 사용되는 허프 그래디언트 방법까지 이해해보자.
허프 변환 직선 검출
직선은 영상에서 찾을 수 있는 많은 특징 중 하나이며 영상 분석에 있어 중요한 정보를 제공한다. 자율 주행 자동차에서 차선을 검출하거나, 수평이 맞지 않는 영상에서 수평선이나 수직선 성분을 찾아내어 자동 영상 회전을 하는 등 다양한 분얃에서 활용된다.
영상에서 직선 정보를 찾기 위해서는
1. 우선 에지를 찾아내야 하고
2. 에지 픽셀들이 일직선상에 배열되어 있는지를 확인해야 한다.
영상에서 직선을 찾기 위한 용도로 허프 변환 (Hough Transform) 기법이 널리 사용되고 있는데, 이는 2차원 xy 좌표에서 직선의 방정식을 파라미터(parameter) 공간으로 변환하여 직선을 찾는 알고리즘이다.
일반적인 2차원 평면에서 직선의 방정식은 다음과 같이 기울기 a, y 절편 b로 (x,y) 좌표를 나타낼 수 있다.

이는 가로축이 x, 세로축이 y인 2차원 xy좌표 공간에 정의되어 있으며, a와 b가 직선의 형태를 결정하는 파라미터라 할 수 있다. 이 수식은 다음과 같이 바꿔 표현할 수 도 있다.

이는 마치 ab 좌표 공간에서 기울기가 -x이고 y절편이 y인 직선의 방정식으로 변경하면, xy 공간에서 직선은 ab 공간에서 한 점으로 표현되고, 반대로 xy 공간에서 한 점은 ab 공간에서 직선의 형태로 나타난다.
xy 좌표 공간과 ab 좌표 공간과의 관계를 다음과 같이 그림으로 표현할 수 있다.

(a)에서 파란색 실선은 xy 공간에서 정의된 직선이며, 이 수식에서 a0과 b0은 직선의 모양을 결정하는 상수이다. xy 공간에서 직선상의 한 점 (x0, y0)을 선택하고, 이 점의 좌표를 이용하면 (b) 그림에 나타난 것과 같이 ab 공간에서 빨간색 직선으로 정의할 수 있다.
마찬가지로 xy 공간에서 같은 직선상의 다른 한 점 (x1, y1)을 이용하면 a, b 공간에서 보라색 직선으로 표현할 수 있다. 이 경우 ab 공간에서 빨간색 직선과 보라색 직선이 서로 교차하는 점의 좌표는 (a0, b0)이며, 이는 xy 공간에서 직선의 방정식 y=a0x+b0을 정의하는 두 파라마티로 구성된 좌표이다.
즉, xy 공간에서 파란색 직선상의 점을 이용해 생성한 ab 공간상의 직선들은 모두 (a0,b0)을 지나간다.
허프 변환을 이용해 직선의 방정식을 찾으려면, xy 공간에서 에지로 판별된 모든 점을 이용하여 ab 파라미터 공간에 직선을 표현하고, 직선이 많이 교차되는 좌표를 모두 찾아야 한다. 이때 직선이 많이 교차하는 점을 찾기 위해 보통 축적 배열 (accumulation array)을 사용한다. 축적 배열은 0으로 초기화된 2차원 배열에서 직선이 지나가는 위치의 배열 원소 값을 1씩 증가시켜 생성한다.
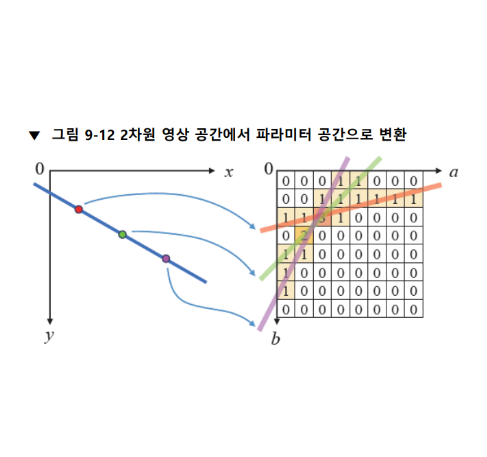
위 그림은 허프 변환에서 축적 배열을 구축하는 방법을 나타낸 그림이다.
왼쪽 xy 영상 좌표게에서 직선 위 3개의 점을 선택하였고, 각 점에 대응되는 ab 파라미터 공간에서의 직선을 오른쪽 배열 위에 나타냈다. 배열 위에서 직선이 지나가는 위치의 원소 값을 1씩 증가시킨 결과를 숫자로 나타낸 것이다.
결과적으로, 오른쪽 그림에 나타난 배열이 축적 배열이고, 축적 배열에서 최댓값을 갖는 위치에 해당하는 a와 b 값이 xy 공간에 있는 파란색 직선의 방정식 파라미터이다.
위는 한 개의 직선에 대해서만 허프 변환한 예이며, 여러 직선이 존재하는 영상의 경우 축적 배열에서 여러 개의 국지적 최댓값 위치를 찾아 직선의 방정식 파라미터를 결정할 수 있다.
그러나 위와 같이 y=ax+b 라는 직선의 방정식을 사용하는 경우 모든 형태의 직선을 표현하기 어렵다는 단점이 있다. 대표적으로 y축과 평행한 수직선은 기울기 a 값이 무한대가 되므로, 을 위 방정식으로는 표현할 수 없다. 따라서 실제 허프 변환을 구할 때는 다음과 같이 극좌표계 형식의 직선의 방정식을 사용한다.

위에서 ρ는 원점에서 직선까지의 수직거리를 나타내고, θ는 원점에서 직선에 수직선을 내렸을 때 x축과 이루는 각도를 의미한다. 따라서 xy 공간에서 한 점은 ρθ 공간에서 삼각함수 그래프 형태의 곡선으로 표현되고, ρθ 공간에서 한 점은 xy 공간에서 직선으로 나타난다. 극좌표계 형식의 직선의 방정식을 사용하여 허프 변환을 수행할 때도 축적 배열을 사용하고, 축적 배열에서 국지적 최댓값이 발생하는 위치에서의 ρ와 θ 값을 찾아 직선의 방정식을 구할 수 있다.
그림으로 나타내면 다음과 같다. xy 좌표계에서 나타난 (a)의 파란색 그림이 ρθ 공간에서 (b)의 곡선과 같은 형태로 나타난다.

ρ와 θ는 실수 값을 가지므로, 각 값이 가질 수 있는 값으 범위를 적당한 크기로 나누어 저장하는 양자화(quantization) 과정을 거쳐야 한다. 예를 들어 θ는 0과 π 사이의 실수를 가지는데, 이 구간을 180단계 또는 360 단계로 나눌 수도 있다. 구간을 촘촘하게 나누는 경우 입력 영상에서 정밀한 직선 검출이 가능해지지만, 연산 시간이 늘어난다.
HoughLines() 함수
OpenCV 에서 HoughLines() 함수를 통해 허프 변환 직선 검출을 수행할 수 있다.

첫번째 인자인 image에는 보통 Canny() 함수 등을 이용해 구한 에지 영상을 지정한다. image 영상에서 0이 아닌 픽셀을 이용해 축적 배열을 구성한다. 직선 파라미터 정보를 받아올 lines 인자에는 보통 vecor<Vector2f> 또는 vector<Vector3f> 자료형의 변수를 지정한다. <Vec3f>로 지정하는 경우 ρ와 θ값 외에 축적 배열에서의 누적 값을 함께 얻어올 수 있다.
rho와 theta 인자는 ρ와 θ 값의 해상도를 조정하는 용도로 사용한다. 예를 들어 rho에 1을 지정하면 ρ 값을 1픽셀로, theta 에 CV_PI/180 을 지정하면 θ를 1˚ 단위로 구분하게 된다. 결과적으로 rho과 tetha 인자가 HoughLines() 함수 내부에서 사용할 축적 배열의 크기를 결정하는 역할을 한다. threshold는 축적 배열에서 직선으로 판단할 임계값을 지정하며, 이 값이 작으면 더 많은 직선이 검출된다.
아래 예제를 살펴보자.
Canny() 함수로 에지 영상을 구하고, 이 영상을 HoughLines() 함수 입력으로 직선을 검출한 뒤,
반환한 직선 파라미터 정보를 이용해 영상 위에 빨간색 직선을 그려 화면에 나타내는 예제이다.
우선 기존 src 영상의 원본, 그리고 Canny 에지 변환을 이용하여 구한 에지 영상은 다음과 같다.


코드는 다음과 같다.
// 허프 변환 직선 검출
void hough_lines() {
Mat src = imread("building.jpg", IMREAD_GRAYSCALE);
if (src.empty()) {
cerr << "Image load failed!" << endl;
return;
}
Mat edge;
Canny(src, edge, 50, 150); // 캐니 에지 검출
// 직선의 방정식 파라미터 정보를 lines에 저장
vector<Vec2f> lines;
HoughLines(edge, lines, 1, CV_PI / 180, 255); // ρ간격은 1픽셀 단위, θ는 1도로 처리
Mat dst;
cvtColor(edge, dst, COLOR_GRAY2BGR); // edge를 컬러 영상으로 변환하여 dst에 저장
// 구해진 직선 lines의 개수만큼 반복문 수행
for (size_t i = 0;i < lines.size();i++) {
float r = lines[i][0], t = lines[i][1]; // 직선의 방정식 파라미터의 p와 θ대입
// 원점에서 직선에 수선을 내렸을 때 만나는 좌표 (x0, y0) 구하기
double cos_t = cos(t), sin_t = sin(t);
double x0 = r * cos_t, y0 = r * sin_t;
double alpha = 1000;
// (x0, y0)에서 충분히 멀리 떨어져 있는 직선 상의 두 점 좌표 저장
Point pt1(cvRound(x0 + alpha * (-sin_t)), cvRound(y0 + alpha * cos_t));
Point pt2(cvRound(x0 - alpha * (-sin_t)), cvRound(y0 - alpha * cos_t));
// 검출된 직선을 빨간색 실선으로 그리기
line(dst, pt1, pt2, Scalar(0, 0, 255), 2, LINE_AA);
}
imshow("edge", edge);
imshow("dst", dst);
waitKey();
destroyAllWindows();
}
HoughLines() 함수로 구하여 얻은 직선 정보들을 담는 lines에는 각 직선에 대하여, 직선의 방정식 파라미터의 ρ와 θ 의 값이 저장되어 있다. 이를 이용해 원점에서 수선의 발을 내려 만나는 좌표 (x0, y0)을 구하고, 이 점에서 충분히 멀리 떨어져 있는 직선 위의 두 점을 구하여 line() 함수를 이용해 빨간색 실선으로 나타냈다.
결과는 다음과 같으며, 왼쪽은 threhold 임계값을 255, 오른쪽은 280로 설정한 결과이다.
임계값이 높아질 수록 더 적은 직선을 검출하는 것을 확인할 수 있다.


HoughLinesP()
OpenCV 에서는 기본적인 허프 변환 직선 검출 방법 외에 확률적 허프 변환 (Probabilistic Hough Transform) 에 의한 직선 검출 방법도 제공한다. 이는 ρ와 θ 의 값을 반환하는 것이 아니라, 직선의 시작점과 끝점 좌표를 반환한다.
즉, 확률적 허프 변환은 선분을 찾는 방법이다.

위 함수에서 검출된 선분 정보가 저장되는 lines 인자에는 vector<Vec4i> 자료형의 변수를 지정한다. Vec4i 객체에는 선분 시작점의 x,y 좌표, 선분 끝점의 x,y 좌표가 저장된다.
maxLineGap 인자는 일직선 상의 직선이 잡음 등 영향으로 끊어졌을 때 두 직선을 하나의 직선으로 간주하고자 할 ㄸ 사용하는 간격 값으로 지정한다.
// 확률적 허프 변환 성분 검출
void hough_line_segments() {
Mat src = imread("building.jpg", IMREAD_GRAYSCALE);
if (src.empty()) {
cerr << "Image load failed!" << endl;
return;
}
Mat edge;
Canny(src, edge, 50, 150);
vector<Vec4i> lines;
HoughLinesP(edge, lines, 1, CV_PI / 180, 160, 50, 5);
Mat dst;
cvtColor(edge, dst, COLOR_GRAY2BGR);
// 선분의 시작점, 끝점 좌표 정보를 이용해 직선 그리기
for (Vec4i l : lines) {
line(dst, Point(l[0], l[1]), Point(l[2], l[3]), Scalar(0, 0, 255), 2, LINE_AA);
}
imshow("src", src);
imshow("dst", dst);
waitKey(0);
destroyAllWindows();
}
결과는 다음과 같다. HoughLines() 함수로 허프 직선 변환 검출을 한 것과는 다르게, 길이가 각각 다른 선분들을 검출한 것을 확인할 수 있다.

허프 변환 원 검출
이번에는 허프 변환을 이용하여 원을 검출해보자. 중심 좌표가 (a,b)이고 반지름이 r인 원의 방정식은 다음과 같이 표현된다.

원의 방정식은 a, b, r 3개의 파라미터를 가지고 있으므로, 허프 변환을 그대로 적용하려면 3차원 파라미터 공간에서 축적 배열을 정의하고 가장 누적이 많은 위치를 찾아야 한다. 그러나 축적 배열을 정의하여 사용하는 경우, 메모리 사용량이 크고 연산 시간을 많이 필요로 하므로, OpenCV에서는 일반적인 허프 변환 대신 그래디언트 방법 (Hough Gradient Method) 을 사용하여 원을 검출한다.
허프 그래디언트 방법은 다음과 같이 두 단계로 구성된다.
1. 영상에서 존재하는 모든 원의 중심 좌표를 찾고
2. 검출된 원의 중심으로부터 원에 적합한 반지름을 구성한다.
중심 좌표를 찾는 과정에서는 축적 배열이 사용된다. 다만 허프 그래디언트 방법에서 사용하는 축적 배열은 파라미터 공간이 아니라, 입력 영상과 동일한 xy 좌표 공간에서 2차원 배열로 만든다. 원의 중심을 찾기 위해 입력 영상의 모든 에지 픽셀에서 그래디언트를 구하고, 그래디언트 방향을 따르는 직선상의 축적 배열 값을 1씩 증가시킨다.

위 그림과 같이, 원주상의 모든 점에 대해 그래디언트 방향의 직선을 그리고, 직선상의 축적 배열 값을 증가시키면 결과적으로 원의 중심 위치에서 축적 배열 값이 가장 크게 나타난다.
원의 중심을 찾은 후, 다양한 반지름의 원에 대해 원주상에 충분히 많은 에지 픽셀이 존재하는지 확인하여 적절한 반지름을 선택한다.
HoughCircles() 함수
허프 변환 원 검출 함수 HoughCirlces() 의 원형은 다음과 같다.

입력 영상에는 에지 영상이 아닌, 원본 그레이스케일 image 영상을 전달한다. HoughCircles() 내부에서 Sobel() 함수와 Canny() 함수를 이용해 그래디언트와 에지 영상을 계산한 후, 허프 그래디언트 방법으로 원을 검출한다.
circles 인자에 vector<Vec3f> 자료형의 변수를 지정하면 중심 좌표(a,b)와 반지름 r이 차례대로 저장되고, <Vec4f>를 지정하는 경우 추가적으로 축적 배열 누적 값이 저장된다. dp 인자에 1을 지정하면 입력 영상과 같은 크기의 축적 배열을, 2를 지정하면 가로와 세로를 각각 2로 나눈 크기의 축적 배열을 사용하게 된다. minDist 에는 인접한 원의 최소 거리를 지정하여, 두 원의 중심점 사이의 거리가 해당 값보다 작으면 두 원 중 하나가 검출되지 않도록 한다.
param1은 캐니 에지 검출기 이용시 높은 임계값으로 사용된다. 낮은 임계값은 param1의 절반으로 설정된다. param2는 축적 배열에서 원의 중심을 찾을 때 사용하는 임계값이다.
검출할 원의 최소, 최대 반지름을 지정하고자 할 때 영상에서 검출할 원의 대략적인 크기를 이미 알고 있다면, minRadius와 maxRadius를 적절히 지정하여 연산 속도를 향상시킬 수 있다.
아래 예제를 살펴보자.
여러 크기의 동전이 있는 영상에서 잡음을 제거한 뒤,
두 원의 중심 점 거리 값을 50픽셀로 설정, 축적 배열의 원소 값이 30보다 큰 경우에 해당하는 허프 변환 원을 검출하고,
검출된 원에 대하여 색상을 달리 하여 영상에 나타도록 했다.
// 허프 변환 원 검출
void hough_circles() {
Mat src = imread("coins.png", IMREAD_GRAYSCALE);
if (src.empty()) {
cerr << "Image load failed!" << endl;
return;
}
Mat blurred;
blur(src, blurred, Size(3, 3)); // 잡음 제거
vector<Vec4f> circles;
// 원 검출 (두 원의 중심점 거리가 50픽셀보다 작으면 검출 X) 캐니 에지 검출기의 높은 임계값은 150으로 지정
// 축적 배열 원소 값이 30보다 크면 원의 중심점으로 선택
HoughCircles(blurred, circles, HOUGH_GRADIENT, 1, 50, 150, 30);
Mat dst;
cvtColor(src, dst, COLOR_GRAY2BGR);
int red_color_value = 50;
int blue_color_value = 255;
for (Vec4f c : circles) {
Point center(cvRound(c[0]), cvRound(c[1]));
int radius = cvRound(c[2]);
cout << c[3] << endl; // 축적 배열의 누적값 출력
// 색상을 달리 하여 검출한 원 그리기
circle(dst, center, radius, Scalar(blue_color_value, 0, red_color_value), 2, LINE_AA);
red_color_value += 40;
blue_color_value -= 50;
}
imshow("src", src);
imshow("blurred", blurred);
imshow("dst", dst);
waitKey(0);
destroyAllWindows();
}
결과는 다음과 같다.

이번에는 두 원의 중심 점 거리 minDist를 100으로 바꾼 결과이다. 가까운 곳에 위치한 일부 동전이 원으로 검출되지 않은 것을 확인할 수 있다. 이를 통해 영상에 나타나는 원들과의 가까운 정도를 미리 알고 있다면 minDist를 적절히 조절하거나, 원의 크기를 미리 알고 있어 minRadius, maxRadius를 적절히 조절한다면 연산량을 효율적으로 줄일 수 있을 것으로 보인다.





