| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- nestjs auth
- 스프링
- OpenCV
- 카카오 알고리즘
- git
- 시스템호출
- 파이썬
- 코테
- thymeleaf
- spring boot
- 프로그래머스
- C++
- @Autowired
- 가상면접사례로배우는대규모시스템설계기초
- @Component
- 해시
- 카카오 코테
- 카카오
- 알고리즘
- AWS
- python
- 컴포넌트스캔
- nestjs typeorm
- C언어
- Spring
- Nodejs
- TypeORM
- 코딩테스트
- nestJS
- 구조체배열
- Today
- Total
공부 기록장 💻
[OpenCV/C++] 영상의 필터링 3 - 샤프닝과 잡음 제거 필터링 본문
[OpenCV/C++] 영상의 필터링 3 - 샤프닝과 잡음 제거 필터링
dream_for 2022. 12. 1. 01:53OpenCV 4로 배우는 컴퓨터비전과 머신 러닝 CH7 필터링 정리
영상 필터링 시리즈
영상의 필터링 1 - 필터 마스크 연산과 엠보싱 필터링 (Embossing) https://dream-and-develop.tistory.com/307
영상의 필터링 2 - 블러링과 가우시안 필터링 https://dream-and-develop.tistory.com/308
영상의 필터링 3 - 샤프닝과 잡음 제거 필터링 https://dream-and-develop.tistory.com/309
샤프닝: 영상 날카롭게 하기
블러링과 반대되는 개념인 샤프닝 (Sharpening) 기법은, 사물의 윤곽이 뚜렷하고 선명한 느낌이 나도록 영상을 변경하는 필터링 기법이다.
언샤프 마스크 필터
샤프닝 기법을 구현하기 위해서는 블러링된 영상을 사용한다. 블러링이 적용된 영상, 언샤프(unsharp)한 영상을 이용하여 역으로 날카로운 영상을 생성하는 필터를 언샤프 마스크 필터(unsharp mask filter)라고 한다.
언샤프 마스크 필터링의 동작 방식을 다음 그림을 통해 이해해보자.
가로 x축은 픽셀 좌표의 이동을, 세로 y축은 픽셀 값을 나타낸다.
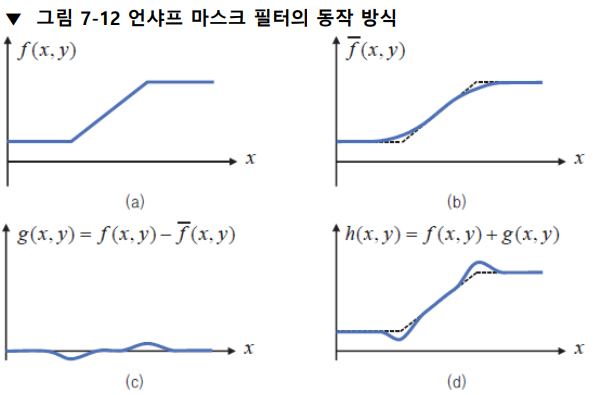
(a)의 경우 영상의 에지 부근에서 픽셀 값이 증가하는 모양을 나타낸 것이고, (b)는 파란색 실선 그래프는 f(x,y)에 블러링을 적용한 결과를 나타낸다.
(c)는 f(x,y)에서 블러링된 영상을 뺸 결과로, 이는 g(x,y)로 표기하였다. 입력 함수 값이 증가하기 시작하는 부분에서는 음수 값을, 입력 함수 값 증가가 멈추는 부근에서는 양수 값을 가진다. 그러므로 f(x,y)에 g(x,y)를 더하면 에지가 강조된 함수가 생성되어, 마지막 (d)에서 h(x,y) = f(x,y) + g(x,y)로 샤프닝이 적용된 결과 영상 그래프를 나타낸다.
결론적으로, (c)의 g(x,y)는 날카로운 성분만을 가지고 있는 함수이므로, 입력 영상 f(x,y)에 g(x,y)를 더함으로써 날카로운 성분이 강조된 최종 영상 h(x,y)가 얻어지는 것으로 해석할 수 있다.
여기서, 실수 가중치를 곱하여 f(x,y)에 g(x,y)를 더하면 날카로운 정도를 사용자가 조절할 수 있게 된다.
샤프닝이 적용된 결과 영상의 수식을 다음과 같이 수정할 수 있다.
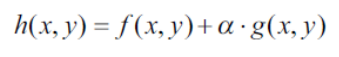
즉, α는 샤프닝 결과 영상의 날카로운 정도를 조절할 수 있는 파라미터이다. 이 값이 1.0이;ㄴ 경우는 날카로운 성분을 그대로 한 번 더하는 셈이고, 1보다 작은 값이라면 조금 덜 날카로운 영상을 만들 수 있다.
위의 수식에서 g(x,y) 을 치환하여 대입하고 식을 정리하면 다음과 같다.
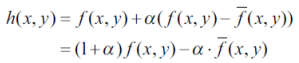
OpenCV는 언샤프 마스크 필터 함수를 따로 제공하지 않는다. 다만 위의 수식을 그대로 소스 코드 형태로 작성하여 샤프닝 결과 영상을 얻을 수 있다.
alpha를 1.F로 지정하고 가우시안 필터링 GaussianBlur을 적용하여 샤프닝 연산을 수행하면 다음과 같이 나타낼 수 있다.
Mat blurred;
GaussianBlur(src, blurred, Size(), sigma);
// unsharp mask (blur 제거)
float alpha = 1.f;
Mat dst = (1 + alpha)*src - alpha * blurred;
전체 코드는 다음과 같다.
// 가우시안 블러링을 이용한 언샤프 마스크 연산
void unsharp_mask() {
Mat src = imread("rose.bmp", IMREAD_GRAYSCALE);
if (src.empty()) {
cerr << "Image load failed!" << endl;
return;
}
imshow("src", src);
for (int sigma = 1;sigma <= 5;sigma++) {
Mat blurred;
GaussianBlur(src, blurred, Size(), sigma);
// unsharp mask (blur 제거)
float alpha = 1.f;
Mat dst = (1 + alpha)*src - alpha * blurred;
String desc = format("sigma :%d", sigma);
putText(dst, desc, Point(10, 30), FONT_HERSHEY_SCRIPT_SIMPLEX,
1.0, Scalar(255), 1, LINE_AA);
imshow("dst", dst);
waitKey();
}
destroyAllWindows();
}
가우시안 필터의 표준 편차 sigma 값을 1부터 5로 증가시키며 샤프닝 연산을 수행한 결과는 다음과 같다.
sigma 값이 커짐에 따라 샤프닝 연산의 결과 영상이 더욱 뚜렷해지는 것을 확인할 수 있다.



잡음 제거 필터링
영상을 획득하는 과정에서 원치 않는 잡음(noise)이 포함될 수 있다. 영상에서 잡음은 주로 영상을 획득하는 과정에서 발생하며, 디지털 카메라로 촬영하는 경우 광학적 신호를 전기적 신호로 변환하는 센서에서 주로 잡음이 추가된다.
컴퓨터 비전 시스템의 전처리 과정으로 잡음 제거 필터를 사용하는데, 다양한 종류의 잡음에 대해 사용할 수 있는 잡음 제거 필터링 기법에 대해 알아보자.
원본 신호를 s(x,y)라 하고, 여기에 추가되는 잡음을 n(x,y)라고 표현할 때 실제로 카메라에서 획득되는 영상 신호 f(x,y)는 다음과 같이 표현한다.
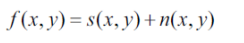
가우시안 잡음 모델
잡음이 생성되는 방식을 잡음 모델(noise model)이라 하며, 다양한 잡음 모델 중에서 가장 대표적인 잡음 모델은 가우시안 잡음 모델(Gaussian noise model)이다. 이는 보통 평균이 0인 가우시안 분포를 따르는 잡음을 의미한다.
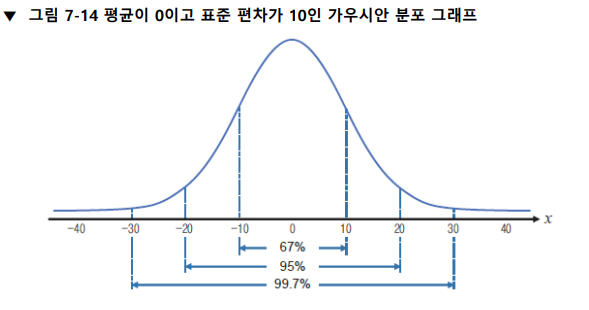
아래와 같이 평균이 0이고 표준 편차가 10인 1차원 가우시안 분포 그래프의 경우, 67%의 확률로 -10과 10 사이의 값이 잡음으로 추가된다. 표준 편차가 작은 가우시안 잡음 모델일수록 잡음에 의한 픽셀 값 변화가 적다고 할 수 있다.
OpenCV 함수를 이용해 영상에 가우시안 모델을 따르는 잡음을 인위적으로 추가하기 위해서는 가우시안 잡음으로 구성된 행렬을 생성하기 위해 randn() 함수를 이용한다.

이때 사용하는 가우시안 분포의 평균은 mean이고 표준 편차가 stddev이다. randn() 함수에 의해 생성된 난수는 dst 행렬의 자료형에 맞게끔 포화 연산이 수행된다.
다음과 같이, lenna 영상에 평균이 0이면서, 표준 편차가 10, 20, 30인 경우의 가우시안 잡음을 영상에 추가해보자.
// 가우시안 잡음 필터링
void noise_gaussian() {
Mat src = imread("lenna.bmp", IMREAD_GRAYSCALE);
if (src.empty()) {
cerr << "Image load failed!" << endl;
return;
}
imshow("src", src);
// 표준 편차가 10, 20, 30인 가우시안 잡음 추가
for (int stddev = 10;stddev <= 30;stddev += 10) {
Mat noise(src.size(), CV_32SC1); // 부호 있는 자료형 행렬 사용
randn(noise, 0, stddev); // 가우시안 잡음으로 구성된 행렬을 생성하여 반환
Mat dst;
add(src, noise, dst, Mat(), CV_8U); // 부호 있는 자료형 행렬 사용
String desc = format("stddev = %d", stddev);
putText(dst, desc, Point(10, 30), FONT_HERSHEY_SCRIPT_SIMPLEX,
1.0, Scalar(255), 1, LINE_AA);
imshow("dst", dst);
waitKey();
}
destroyAllWindows();
}
다음과 같이, 원본 영상에 비해 가우시안 잡음이 추가된 결과 영상은 거칠고 지저분해 보이며,
표준 편차 값이 증가함에 따라 잡음의 영향이 커지는 것을 확인할 수 있다.



양방향 필터
대부분의 영상에는 가우시안 잡음이 포함되어 있으며, 많은 컴퓨터 비전 시스템은 이를 제거하기 위해 가우시안 필터를 사용한다. 입력 영상에서 픽셀 값이 크게 변하지 않는 평탄한 영역에 가우시안 필터가 적용되는 경우, 주변 픽셀 값이 부드럽게 블러링 되며 잡음의 영향도 줄어든다. 그러나 픽셀 값이 급격히 변경되는 에지 근방에 동일한 가우시안 필터가 적용되면 잡음 뿐 아니라 에지 성분까지 감소한다. 따라서, 잡음이 줄어듬과 동시에 에지도 무뎌져 객체의 윤곽이 흐려진다.
이 단점을 보완하기 위해, 에지 정보는 그대로 유지하며 잡음만 제거하는 에지 보전 잡음 제거 필터 (edge-preserving noise removal filter)에 대해 연구가 되었다.그 중 하나인 양방향 필터(bilateral filter)은 에지 성분은 그대로 유지하며 가우시안 잡음을 효과적으로 제거하는 알고리즘이다.
이 필터는 다음 공식을 사용해 필터를 수행한다.
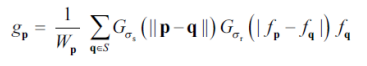
위 수식은, 두 점의 픽셀 밝기 값의 차이가 적은 평탄한 영역에서는 큰 가중치를 갖게 만든다. 반면 에지를 사이에 두고 있는 두 픽셀에 대해서는 상대적으로 두 점의 픽셀 밝기 값이 크게 나타나 두 점의 픽셀 값에 의한 가중치가 거의 0에 가까워, 에지 근방에서는 가우시안 블러링 효과가 거의 나타나지 않고 에지가 보존된다.
양방향 필터 수식이 픽셀 값의 차이에 의존적이므로 이는 모든 픽셀에서 서로 다른 형태를 갖게 된다. 즉 모든 픽셀 위치에서 주변 픽셀과의 밝기 차이에 의한 고유의 필터 마스크 행렬을 만들어 마스크 연산을 수행해야 한다. 따라서 가우시안 블러링보다 훨씬 많은 연산량을 필요로 한다.
bilateralFilter() 함수
OpenCV 에서는 bilateralFilter() 함수를 이용해 양방향 필터를 수행한다.
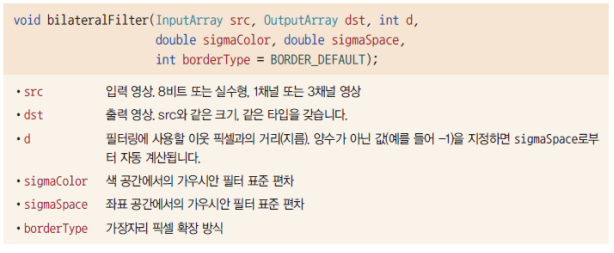
sigmaSpace 값은 일반적인 가우시안 필터링에서 사용하는 표준 편차와 같은 개념으로, 값이 클수록 더 많은 주변 픽셀을 고려하여 블러링을 수행하게 된다.
sigmaColor은 주변 픽셀과의 밝기 차이에 관한 표준 편차이다. 이를 작게 지정할 경우, 픽셀 값 차이가 큰 주변 픽셀과는 블러링 연산이 적용되지 않는다. 따라서 이 값을 이용해 어느 정도 밝기 차를 갖는 에지를 보존할 것인지를 조정할 수 있다.
// 양방형 필터링을 이용한 잡음 제거
void filter_bilateral() {
Mat src = imread("lenna.bmp", IMREAD_GRAYSCALE);
if (src.empty()) {
cerr << "Image load failed!" << endl;
return;
}
imshow("src", src);
Mat noise(src.size(), CV_32SC1);
randn(noise, 0, 5); // 표준 편차 5인 가우시안 잡음 추가
add(src, noise, src, Mat(), CV_8U);
Mat dst1;
GaussianBlur(src, dst1, Size(), 5);
Mat dst2;
// sigmaColor 표준 편차 10, sigmaSpace 표준 편차 5로 설정
bilateralFilter(src, dst2, -1, 10, 5);
imshow("src", src);
imshow("dst1", dst1);
imshow("dst2", dst2);
waitKey();
destroyAllWindows();
}
표준 편차가 5인 가우시안 잡음이 추가된 lenna 영상에 대하여,
가우시안 블러링을 이용한 잡음 제거 결과 영상인 dst1는 잡음은 줄었지만 전체 경계가 블러링되어 흐릿하게 변경된 반면,
양방향 필터링 연산의 결과 영상인 dst2는 머리카락, 모자, 배경 사물의 경계는 그대로 유지되며, 평탄안 영역의 잡음이 크게 줄어들어 눈으로 보기에 깔끔한 결과 영상을 만들었음을 확인할 수 있다.



미디언 필터
미디언 필터(median filter)는 입력 영상에서 자기 자신 픽셀과 주변 픽셀 값 중에서 중간값(median)을 선택하여 결과 영상 픽셀 값으로 설정하는 필터링 기법이다. 이는 마스크 행렬과 입력 영상 픽셀 값을 서로 곱한 후 모두 더하는 형태의 연산이 아니라, 주변 픽셀 값들의 중간값을 선택하기 위해 내부에서 픽셀 값 정렬 과정이 사용된다.
미디언 필터는 특히 잡음 픽셀 값이 주변 픽셀 값과 큰 차이가 있는 경우 효과적으로 동작한다.
영상에 추가되는 잡음 중 소금&후추 잡음 (salt & pepper noise) 은 픽셀 값이 일정 확률로 0 또는 255로 변경돠는 형태의 잡음이다. 소금&후추 잡음이 추가된 영상에 미디언 필터를 적용하면 대부분 원본 영상에 존재하는 픽셀 값이 중간값으소 선택되기 때문에 잡음이 효과적으로 제거된다.
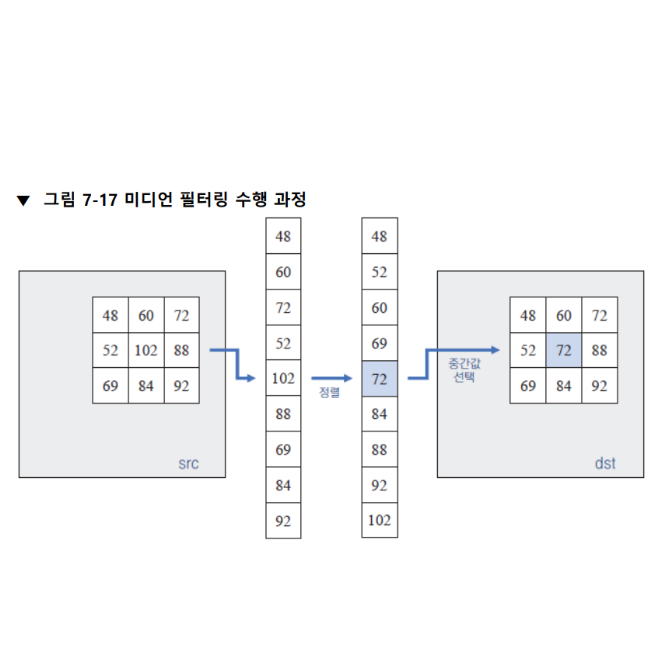
3x3 정방형 마스크를 사용하는 미디언 필터의 경우 다음과 같이 동작한다. 영상의 특정 위치에서 3x3 주변 픽셀 값 배열을 일렬로 늘여 세운 후, 픽셀 값을 크기 순으로 정렬한 뒤 데이터에서 중앙에 있는 픽셀 값인 72를 선택하여 결과 영상의 픽셀 값으로 설정한다. 이 과정을 영상 전체 픽셀에 대해 수행하면 미디언 필터 결과 영상이 만들어 진다.
medianBlur() 함수
OpenCV에서는 medianBlur() 함수를 이용해 미디언 필터링을 수행한다.
ksize x ksize 필터 크기를 이용해 미디언 필터링을 수행하여, 3보다 같거나 큰 홀수를 지정해야 한다.
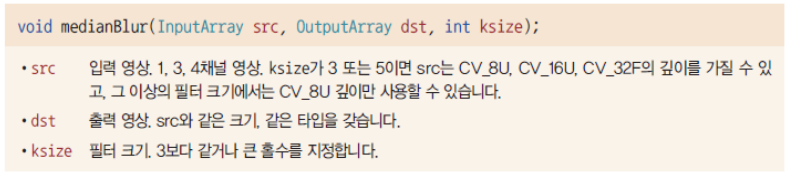
다채널 영상의 경우 각 채널별로 필터링을 수행하고, 함수는 내부적으로 BORDER_REPLICATE 방식으로 가장자리 외각 픽셀 값을 설정하여 필터링을 수행한다.
// 미디언 필터링 연산을 이용한 잡음 제거
void filter_median() {
Mat src = imread("lenna.bmp", IMREAD_GRAYSCALE);
if (src.empty()) {
cerr << "Image load failed!" << endl;
return;
}
imshow("src", src);
// 입력 영상 전체 크기의 10% 에 해당하는 픽셀에 소금&후추 잡음을 추가
// 솔트앤패퍼 잡음
int num = (int)(src.total()*0.1);
for (int i = 0;i < num;i++) {
int x = rand() % src.cols;
int y = rand() % src.rows;
src.at<uchar>(y, x) = (i % 2) * 255; // 랜덤 위치에 0 또는 255로 픽셀 지정
}
// 가우시안 잠음 필터 수행
Mat dst1;
GaussianBlur(src, dst1, Size(), 1);
// 미디언 잡음 필터 수행
Mat dst2;
medianBlur(src, dst2, 3); // 3x3 필터 크기를 이용해 미디언 필터링 수행
imshow("src", src);
imshow("dst1", dst1);
imshow("dst2", dst2);
waitKey();
destroyAllWindows();
}
결과는 다음과 같다. lenna 영상의 10%의 확률로 소금&후추 잡음이 추가되었다. (0 검정 또는 255 흰색의 잡음)
Gaussian Blurring이 적용된 dst1는 여전히 지저분한 결과 영상으로 나타나지만,
Median Filtering을 적용한 dst2의 경우 잡음 픽셀이 효과적으로 제거되어 깨끗한 결과 영상이 나타남을 확인할 수 있다.




